推荐系统学习(CTR预估)
CTR预估
FM 因子分解机
介绍:
作为逻辑回归模型LR的改进版,拟解决在稀疏数据的场景下模型参数难以训练的问题。并且考虑了特征的二阶交叉,弥补了逻辑回归表达能力差的缺陷。
原理:
在线性模型的基础上添加了一个多项式(最后一项),用于描述特征之间的二阶交叉。但是参数学习困难,因为对 进行更新时,求得的梯度对应为、 ,当且仅当二者都非 0 时参数才会得到更新。因此引入辅助向量,使用内积:
引入辅助向量削弱了参数间的独立性,只要不是0,参数就可以得到更新。解决了数据稀疏带来的难以训练问题。
在时间复杂度上,可以从优化到,更利于上线使用
同时,也可以拓展到多维空间:
跟二阶交叉项相同,多阶交叉项也可从 复杂度降到线性的 ,具有非常好的性质。
优点:
- 将二阶交叉特征考虑进来,提高模型的表达能力;
- 引入隐向量,缓解了数据稀疏带来的参数难训练问题;
- 模型复杂度保持为线性,并且改进为高阶特征组合时,仍为线性复杂度,有利于上线应用。
缺点:
- 虽然考虑了特征的交叉,但是表达能力仍然有限,不及深度模型;
- 同一特征 与不同特征组合使用的都是同一隐向量 ,违反了特征与不同特征组合可发挥不同重要性的事实。
FFM
论文链接:FFM
介绍:
一个特征在跟不同特征作交互时,会发挥不同的作用,因此应该具有不同的向量表示,解决了FM同一隐向量问题
原理:
FFM 将隐向量进一步细分,每个特征具有多个隐向量 (等于 field 的数目)。公式如下:
表示特征 与 特征$ j$ 交互时的隐向量表示,其中 表示第 个特征所属的 field。
模型参数量为 , 为 field 数。公式不可化简,复杂度为 。
优点:
- 引入 field 域的概念,让某一特征与不同特征做交互时,可发挥不同的重要性,提升模型表达能力;
- 可解释性强,可提供某些特征组合的重要性。
缺点:
- 复杂度高,不适用于特征数较多的场景。
Wide & Deep
论文链接:Wide&Deep
介绍:
在此之前,CTR任务中主要以线性模型+人工特征为主流方法,此类方法缺陷比较明显:线性模型表达能力有限,需要大量人工特征来提升模型效果。随着深度学习的不断火热,深度模型展现了强大的表达能力,并且能自适应的学习特征之间的高阶交互。
因此 Google 取彼之长补己之短,将线性模型与深度模型以并行结构的方式进行融合,线性部分拟提取低阶交互信息,深度部分提取高阶交互信息,提出了 Wide&Deep模型,并在Google Play store中成功落地,收益明显。
原理:
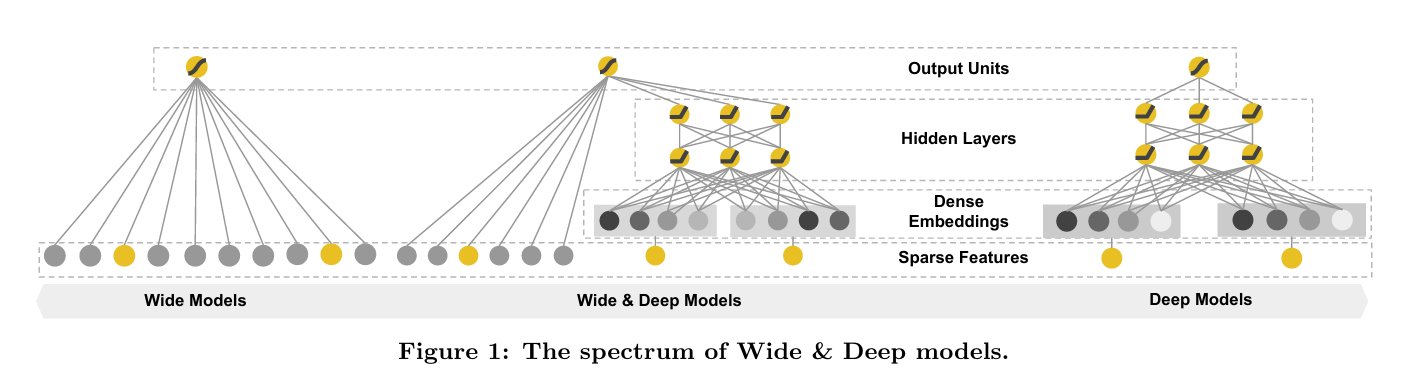
括号内第一项为线性模型的输出,第二项为深度模型的输出,将两部分输出相加,再加上一个偏置$ b $之后输入 sigmoid 进行激活得到预测的概率值。
Wide部分
线性部分等同于一个 LR,唯一不同的是在输入上多了 ,该项表示的是在原始输入 上构造出的人工特征,一般为特征之间的二阶交互,也可根据业务场景设计一些复杂的强特征,以提升模型表达能力。
线性部分的输出是对输入 的线性映射,无需激活。
Deep部分
该部分为一个多层的全连接网络,第 层的输出为 , 为全连接最后一层未进行 sigmoid 激活的输出,与线性部分未激活的输出相累加再进行激活即为模型最终输出。
需要注意的是,两部分的输入不同:
Wide 部分:Dense Features + Sparse Features(onehot 处理)+ 特征组合
Deep 部分:Dense Embeddings (Sparse Features 进行 onehot + embedding 处理)
优点:
-
结构简单,复杂度低,目前在工业界仍有广泛应用;
-
线性模型与深度模型优势互补,分别提取低阶与高阶特征交互信息,兼顾记忆能力与泛化能力;
-
线性部分为广义线性模型,可灵活替换为其他算法,比如 FM,提升 wide 部分提取信息的能力。
缺点:
-
深度模型可自适应的进行高阶特征交互,但这是隐式的构造特征组合,可解释性差;
-
深度模型仍需要人工特征来提升模型效果,只是需求量没有线性模型大。
DeepFM
论文链接:DeepFM: A Factorization-Machine based Neural Network for CTR Prediction
介绍:
DeepFM 是 Deep 与 FM 结合的产物,也是 Wide&Deep 的改进版,只是将其中的 LR 替换成了 FM,提升了模型 wide 侧提取信息的能力。
原理:
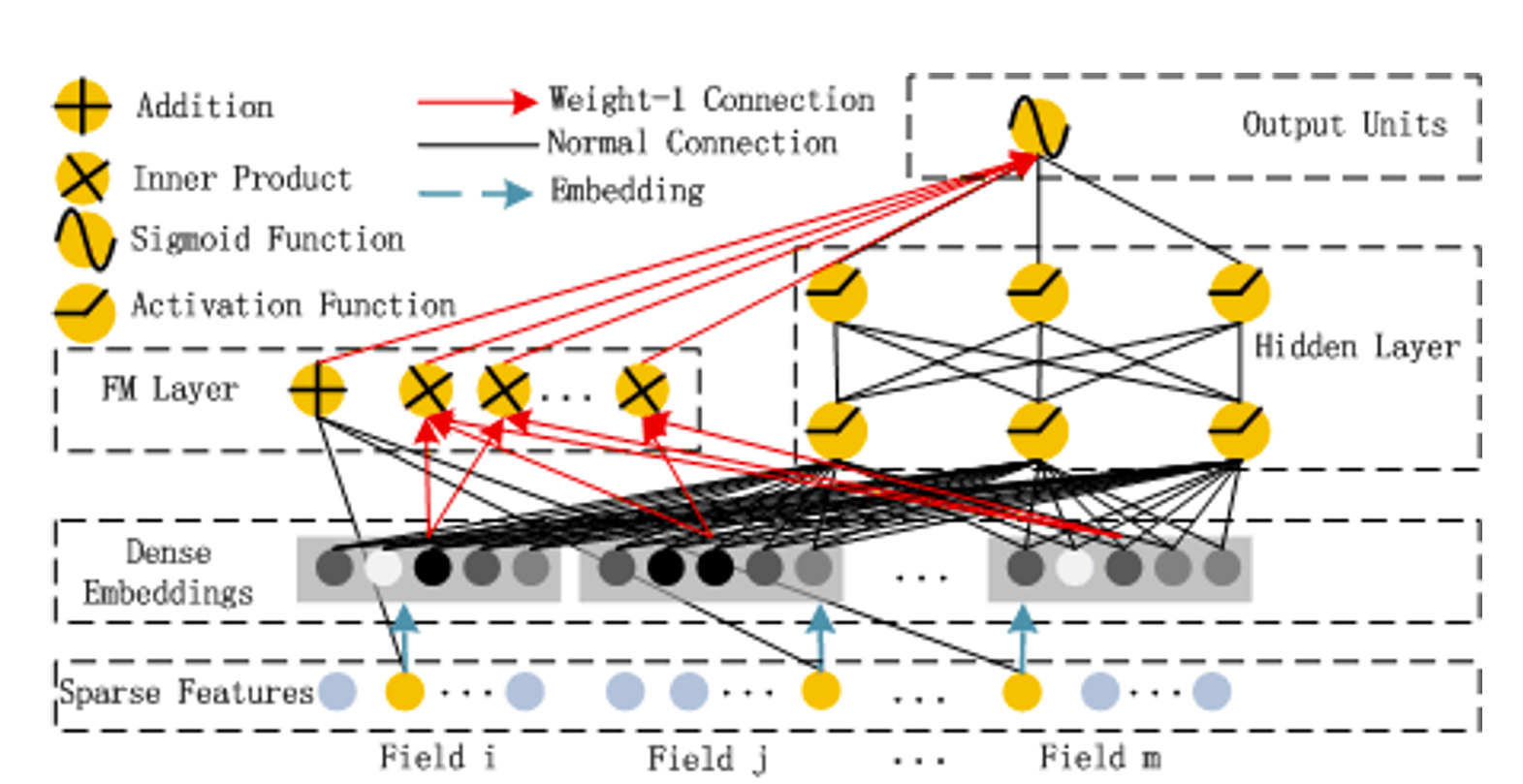
Sparse Features
一般类别特征无法直接输入模型,所以需要先 onehot 处理得到的其稀疏01向量表示。该层即表示经过 onehot 编码的类别特征与数值特征的拼接。
Dense Embeddings
该层为嵌入层,用于对高维稀疏的 01 向量做嵌入,得到低维稠密的向量 e (每个01向量对应自己的嵌入层,不同向量的嵌入过程相互独立,如上图所示)。然后将每个稠密向量横向拼接,在拼接上原始的数值特征,然后作为 Deep 与 FM 的输入
FM Layer
FM 有两部分,线性部分和交叉部分。线性部分 (黑色线段) 是给与每个特征一个权重,然后进行加权和;交叉部分 (红色线段) 是对特征进行两两相乘,然后赋予权重加权求和。然后将两部分结果累加在一起即为 FM Layer 的输出。
Hidden Layer
Deep 部分的输入 为所有稠密向量的横向拼接,然后经过多层线性映射+非线性转换得到 Hidden Layer 的输出,一般会映射到1维,因为需要与 FM 的结果进行累加。
Output Units
输出层为 FM Layer 的结果与 Hidden Layer 结果的累加,低阶与高阶特征交互的融合,然后经过 Sigmoid 非线性转换,得到预测的概率输出。
优点:
-
两部分联合训练,无需加入人工特征,更易部署;
-
结构简单,复杂度低,两部分共享输入,共享信息,可更精确的训练学习。
缺点:
- 将类别特征对应的稠密向量拼接作为输入,然后对元素进行两两交叉。这样导致模型无法意识到域的概念,FM 与 Deep 两部分都不会考虑到域,属于同一个域的元素应该对应同样的计算。
Deep&Cross(DCN)
介绍:
把 wide 侧的 LR 换成了 cross layer,可显式的构造有限阶特征组合,并且具有较低的复杂度。
原理:
通过显式交叉⽹络(Cross Layer)⽣成⾼阶特征,替代Wide部分的交叉特征⼯程。
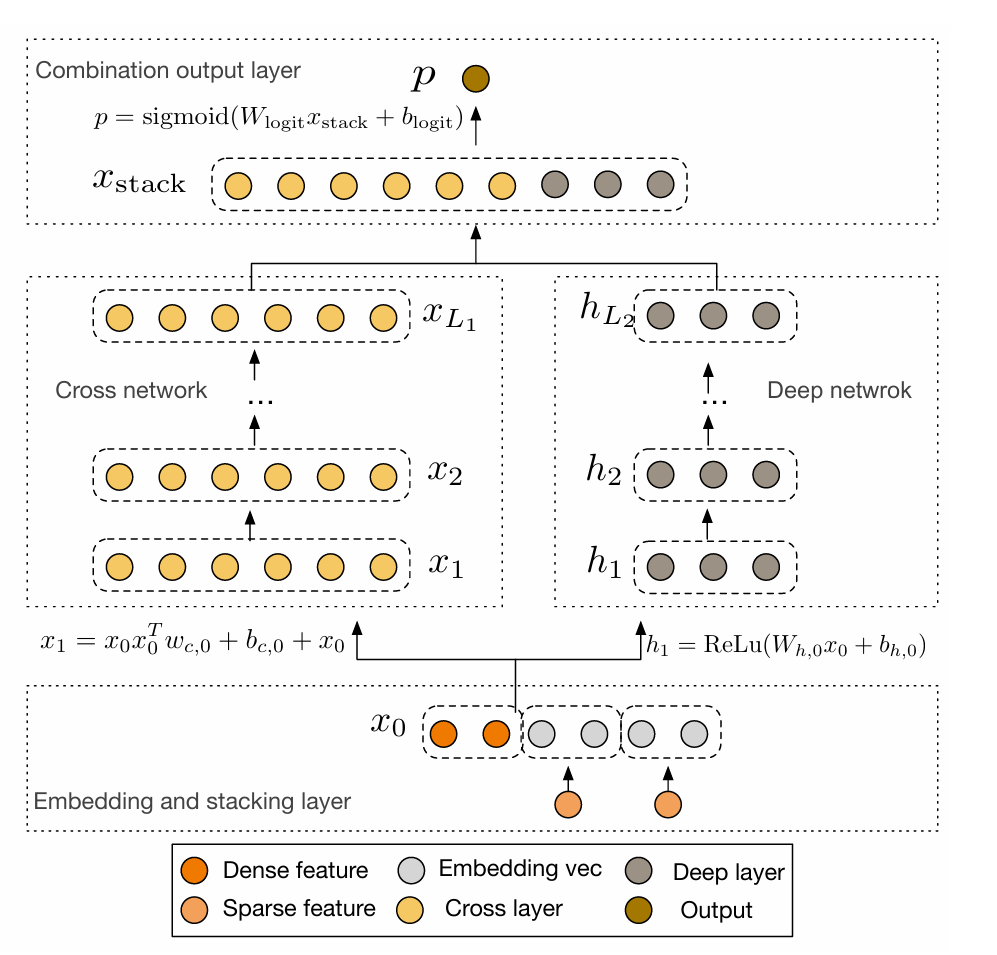
优点:
- 引入 cross layer 显示的构造有限阶特征组合,无需特征工程,可端到端训练;
- cross layer 具有线性复杂度,可累加多层构造高阶特征交互,并且因为其类似残差连接的计算方式,使其累加多层也不会产生梯度消失问题;
- 跟 deepfm 相同,两个分支共享输入,可更精确的训练学习。
缺点:
cross layer 是以 bit-wise 方式构造特征组合的,最小粒度是特征向量中的每个元素,这样导致 DCN 不会考虑域的概念,属于同一特征的各个元素应同等对待;
其它
以上介绍的 DCN 也叫作 DCN-vector。
改进版DCN-matrix 将 cross layer 中做线性映射的向量 替换成了矩阵,并且为了不引入过多的参数量,作者又将 矩阵分解成了两个高瘦矩阵的乘积,并且在第一个矩阵映射后还可以加一个激活函数进行非线性转换,以此来提高模型的表达能力,这就是 DCN-matrix 相对于 DCN-vector 的不同之处。
DCN-matrix 也提出了一种串行拼接方式,就是将 cross layer 最后一层的输出作为 deep layer 的输入,串行的拼接两部分。串行与并行拼接方式在不同场景中表现不同,说不上孰好孰坏。
xDeepFM
论文链接: xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems
介绍
xDeepFM 是 Wide & Deep 的改进版,在此基础上添加了 CIN 层显式的构造有限阶特征组合。xDeepFM 虽然名字跟 DeepFM 类似,但是两者相关性不大。
原理:
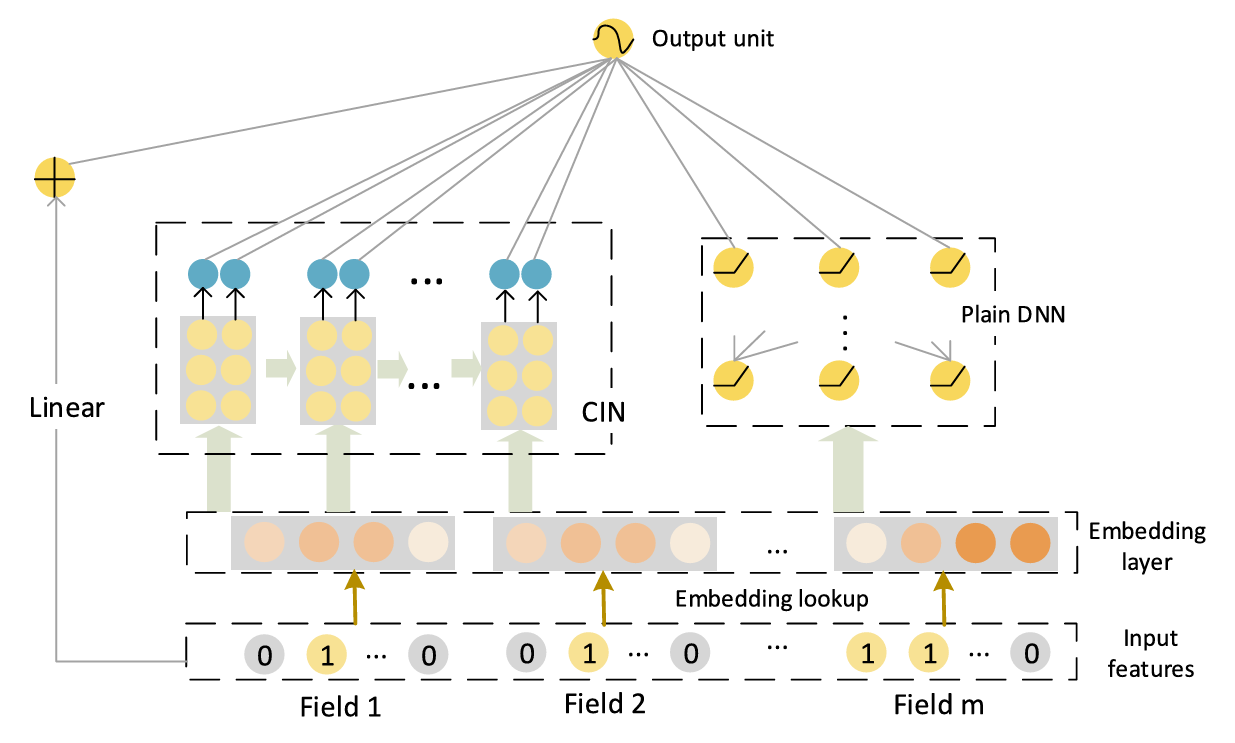
有三个分支:Linear(稀疏的01向量作为输入)、DNN(经过embedding的稠密向量作为输入)、CIN。xDeepFM 如果去掉 CIN 分支,就等同于 Wide & Deep
CIN
-
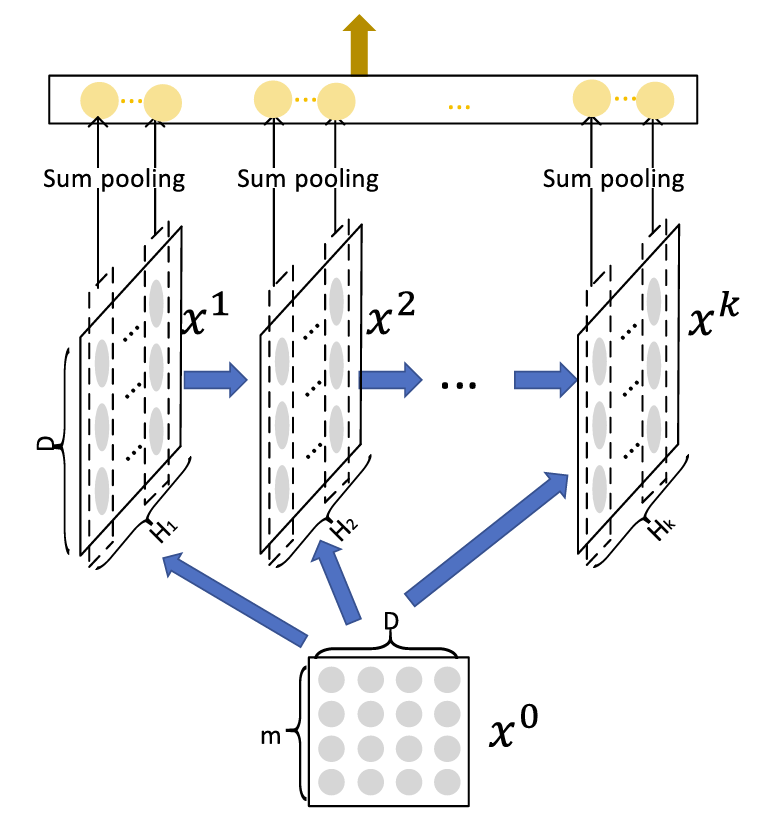
CIN 的输入是所有 field 列向量横向拼接得到的矩阵 $X_0∈Rm∗D $( m 个维度为 D 的 field 向量)。并且后续的每层特征组合都是形状都是 ,每层的特征个数 不再相同,维度 D 始终保持不变;
-
每次第 i 层的特征矩阵 都会与原始输入 做交互,得到第 层的特征矩阵 ,具体交互方式:
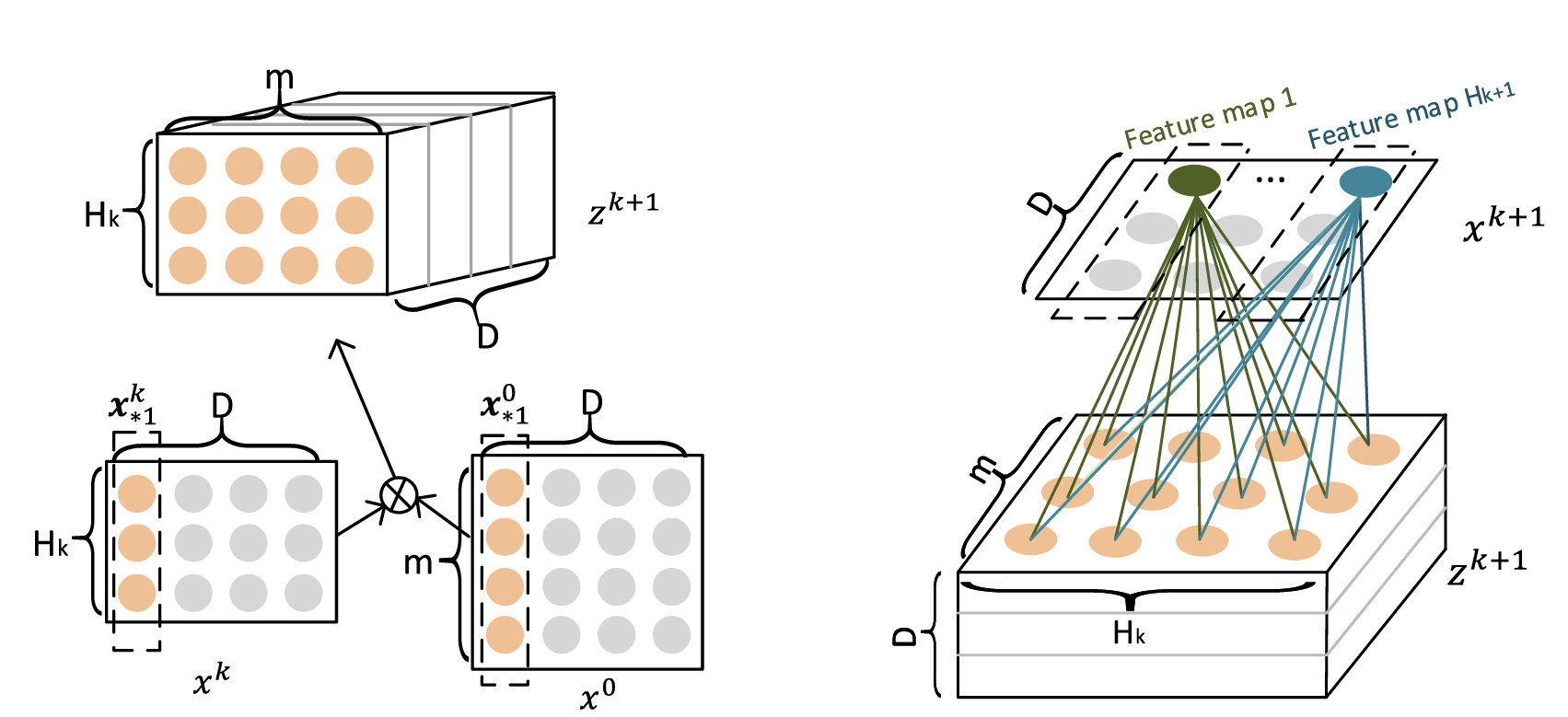
-
矩阵 与 分别是含有 和个 D 维特征的矩阵;
-
两个矩阵中的特征两两做对应元素乘积,会得到 个 D 维特征,这样就实现了特征交互(图中画出的框框是内积计算方式,不好理解);
-
这些交互特征不是直接拼接成形状为 的特征矩阵,而是拼接成三维矩阵 ;
-
**得到三维矩阵后,**使用一个形状为 权重矩阵 ,分别与三维矩阵中 个同形状的矩阵做元素乘积,每次乘积之后求和得到一个标量,然后将每个标量 concat 到一起,最终得到一个维度为 D 的向量;
-
使用 个不同的权重矩阵 ,即可得到 不同的 D 维向量,拼接在一起即为下一层的特征矩阵 。
-
-
因为每一层只包含某一阶的特征组合,所以每一层的特征矩阵都会被使用来对最终结果作预测,将每层特征矩阵的 Hi 个特征在 D 维度做 sum pooling, 总共会得到 个标量,concat 拼接在一起得到的一维向量作为 CIN 层的输出,后续与 Linear 和 DNN 部分的输出拼接做最终的预测。
(因为每次矩阵 W 都会将特征两两交互得到的三维矩阵压缩成一维,所以叫做压缩感知)
优点:
使用 vector-wise 的方式,通过特征的元素积来进行特征交互,将一个特征域的元素整体考虑,比 bit-wise 方式更 make sence 一些;
缺点:
CIN 层的复杂度通常比较大,它并不具有像 DCN 的 cross layer 那样线性复杂度,它的复杂度通常是平方级的,因为需要计算两个特征矩阵中特征的两两交互,这就给模型上线带来压力。
FNN
介绍
也是 FM 与 DNN 结合的产物,不同的是,FNN 采用的是串行拼接的结合方式,将 DNN 接在 FM 层后方,以减轻全连接层构造隐式特征的工作。
原理
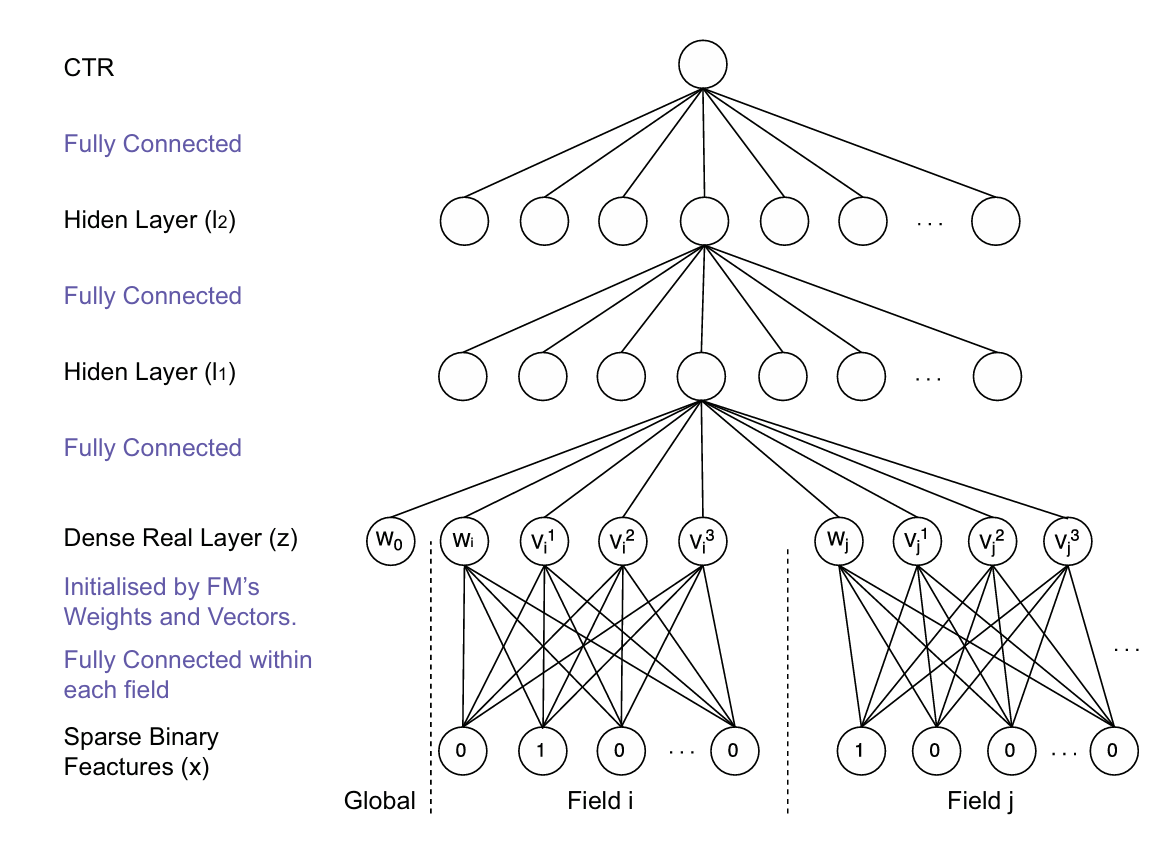
Sparse Binary Features
模型的原始输入为稀疏的 0-1 向量,由稠密的数值特征和经过 onehot 处理得到的类别特征拼接而成,图中一个 field 表示一个经过 onehot 的类别特征。
Dense Real Layer
该层为嵌入层,作用是将每个 field 中的稀疏 01 向量,单独映射得到低维稠密特征(图中为 4 维的稠密特征,即 FM 隐向量的维度)。跟一般的Embedding 嵌入层不同是,该嵌入层的权重由 FM 训练得到的隐向量初始化得到。
每个 field 的输入为一个 01 向量,只有一个特征的取值为 1,乘上嵌入矩阵即可得到该特征对应的隐向量,数值特征直接乘上自己的隐向量即可,然后将所有 field 映射得到的隐向量 concat 作为全连接的输入即可。(相当于输入的每维特征都乘上自己对应的隐向量,只不过每个 field 只会得到一个隐向量,然后横向拼接所有隐向量即为输入)
Hidden Layer
标准的三层全连接,最后一层映射到一维接 sigmoid 得到概率输出,即为预测的 CTR 概率。
优点:
- 将 FM 学习得到的隐向量作为 DNN 的输入,隐向量包含了 FM 习得的先验知识,可减轻 DNN 的学习压力;
- FM 只考虑到了二阶特征交互,忽略了高阶特征,后面接 DNN 可弥补该缺陷,提升模型表达能力。
缺点:
- 采用两阶段、非端到端的训练方式,不利于模型的线上部署;
- 将 FM 的隐向量直接拼接作为 DNN 的输入,忽略了 field 的概念;
- FNN 未考虑低阶特征组合,低阶、高阶特征是同等重要的。
PNN
论文链接:PNN
介绍
通过引入特征交互层Product Layer,显式的对特征进行交互,以提升模型的表达能力。
原理:
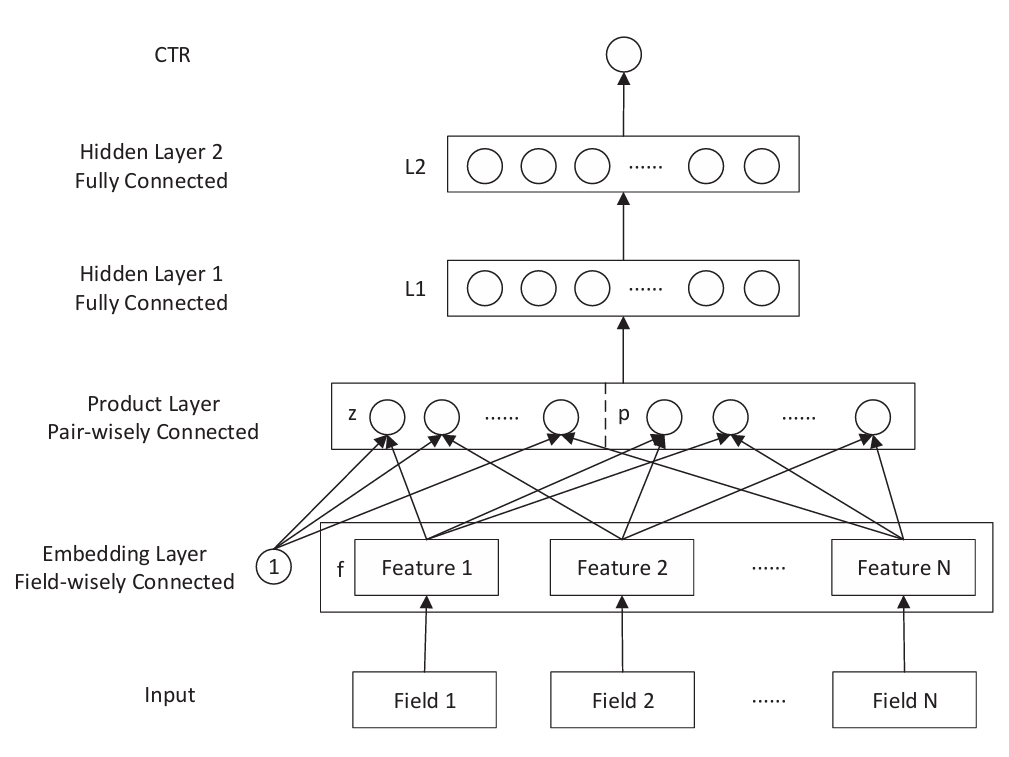
Embedding Layer
该层为嵌入层,用于将 input 中的每个 Field 特征映射成低维稠密特征,然后每个特征的 embedding 横向拼接,作为下一层的输入。
Product Layer
该层为特征交互层,由 z 和 p 两部分组成,其中 z 为上层的输出结果,p 为上层输出的特征交互结果,低维与高维特征的直接拼接。
Product Layer 以 Field 为粒度进行特征之间的交叉,交叉方式有两种:内积 IPNN 和 外积 OPNN。
Embedding Layer输出的张量形状为 [None, field, k],其中 None 表示 batchsize 大小,field 为原始输入的特征个数,k 为每个特征嵌入之后对应稠密向量维度。
Inner Product:
filed 个特征两两进行内积,每两个 k 维特征的内积可得到一个一维变量,总共可得到 field * (field-1) / 2 个变量,拼接在一起即为特征交互的结果 p,形状为 [None,field * (field-1) / 2] 。
Outer Product:
与内积不同的是,每两个 k 维特征的外积不再是一个一维变量,而是形状为 [k, k] 的二维张量。
所以又引入等形状的权重矩阵 W,与二维张量进行对应元素乘积,然后求和得到一维变量。
文中引入 field * (field-1) / 2 个可训练的权重矩阵,与每个二维张量计算元素积,得到 field * (field-1) / 2 个变量,然后拼接得到特征交互的结果 p,形状跟内积结果相同,也为 [None,field * (field-1) / 2] 。
外积与内积的唯一差别,就是多了一次矩阵的元素积计算。
得到特征交互结果之后,与上层输出 z 拼接即为 Product Layer 层的输出。
Tips: 内积与外积两种特征交互方式可同时使用,把内积外积的交互结果横向拼接即可。
Hidden Layer
三层全连接,最后一层映射到一维接 sigmoid 得到概率输出,即为预测的 CTR 概率。
优点:
- 显式的进行特征交互,提高模型表达能力;
- 以 field 为粒度进行特征交互,保留的域的概念;
- 同时保留了低维与高维特征
缺点:
- 外积交互方式参数量较大,随着特征维度平方级增长;
DIN
论文链接:DIN
介绍:
通过引入 Attention Layer,赋予用户行为不同的重要性权重,获得更具表达能力的用户兴趣表示。
原理:
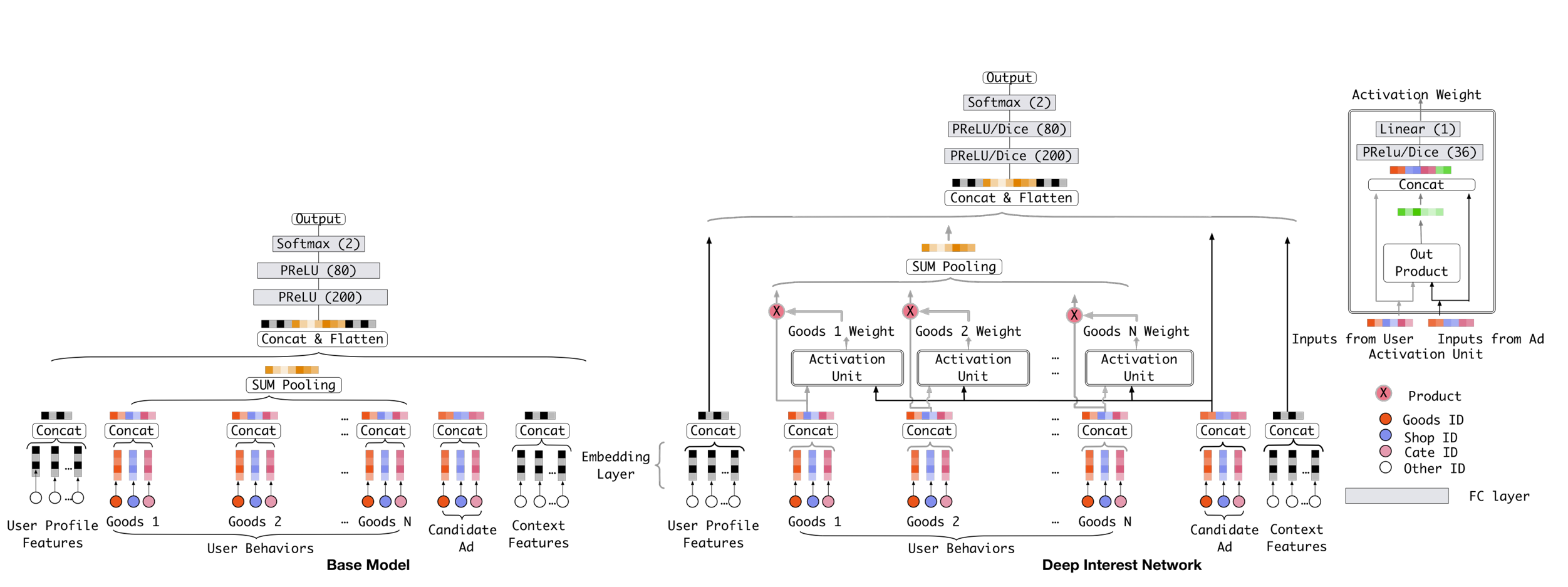
阿里的推荐系统主要用到四组特征:用户画像特征、用户行为特征、候选商品、上下文特征。本文只需关注用户行为特征如何处理即可。Base 模型的做法是将用户点击的商品序列,简单的进行 SUM Pooling,然后将聚合得到的 embedding 向量,作为用户的兴趣表示。这种做法的缺陷也很明显,简单的累加无法突出某些商品的重要性。对于与候选商品具有强关联性的 item,应该给予更大的权重,让其在提取用户兴趣时发挥更大的作用。
Activation Unit
主要关注 Activation Unit 内的权重计算方式,该单元的输入为:用户点击的商品(Inputs from User)、候选商品(Inputs from Ad)。
- 计算点击的商品与候选商品的外积,得到一维embedding;
- 将外积结果与原始输入 Concat 在一起;
- 后面结两层全连接,隐层激活函数使用 PRelu或Dice,输出映射到一维,表示权重分数。
用户点击的多个商品,分别按照以上方式与候选商品计算权重,然后加权再取 SUM Pooling 即可。这样就突出了重要商品发挥的作用,可提取到更精确的用户兴趣表示。
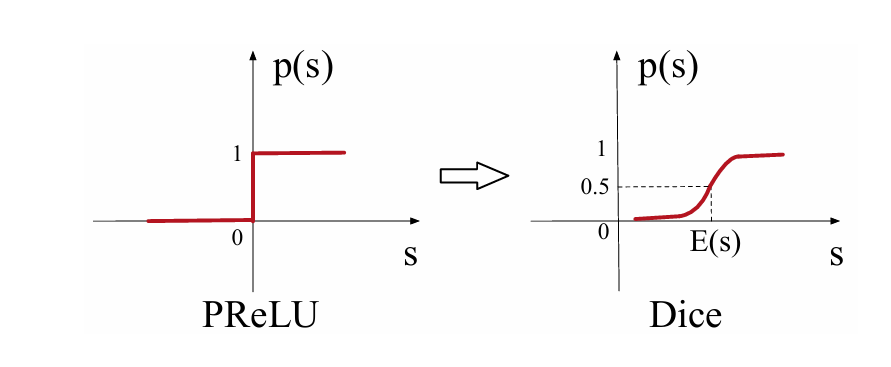
Dice 激活函数是对 PRelu 的改进。因为 Relu、PRelu 的梯度发生变化的点都固定在 x=0 处,神经网络每层的输出往往具有不同分布,所以固定在一处无法适应多样的分布,所以变化点应随着数据的分布自适应调整。
优点:
- 引入 Attention 机制,更精准的提取用户兴趣;
- 引入 Dice 激活函数与,并优化了稀疏场景中的 L2 正则方式。
缺点:
- 没有考虑用户点击商品的相对位置信息,后续的 DIEN 也是针对这点进行了改进。
DIEN
论文链接:DIEN
介绍:
针对行为的时间顺序进行建模,挖掘用户的兴趣及兴趣变化趋势。
原理
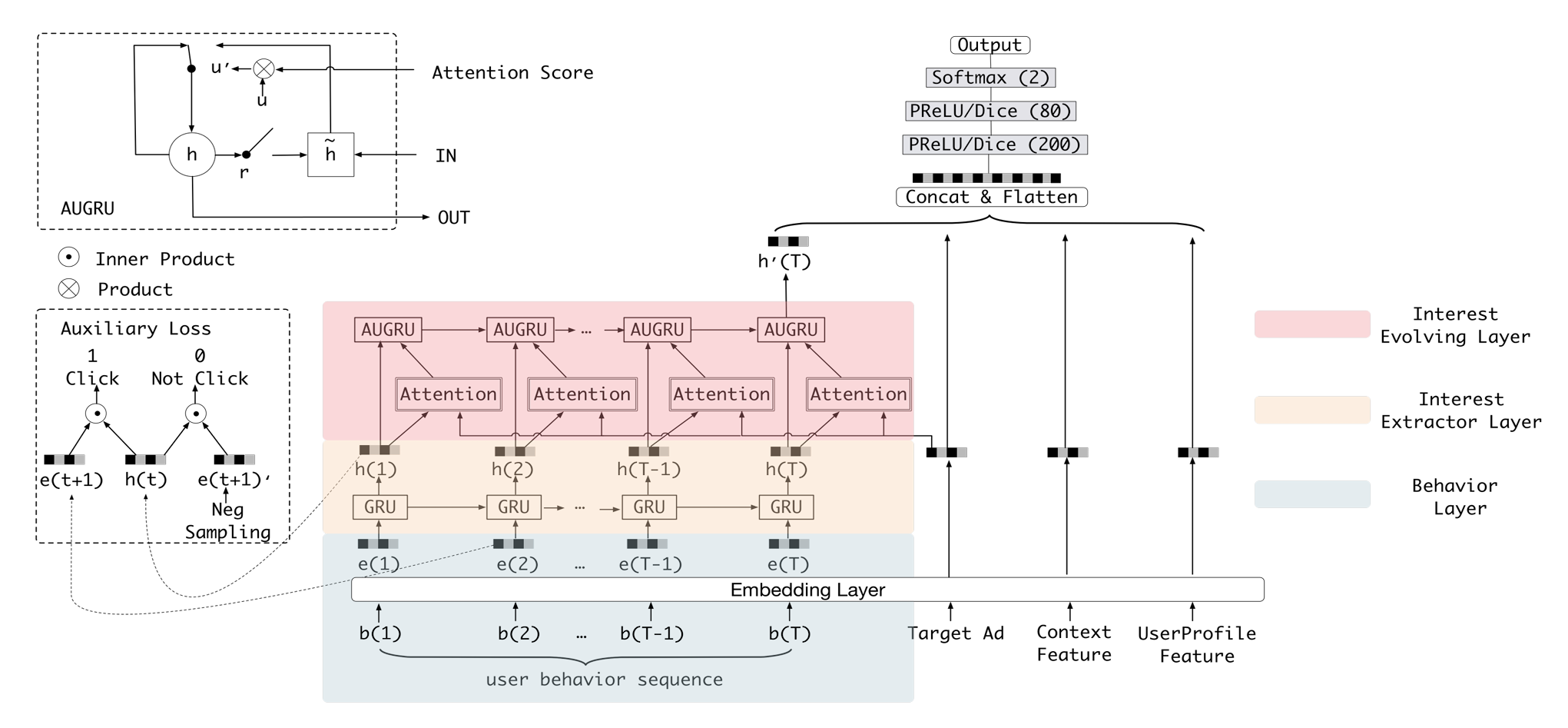
Behavior Layer
嵌入层,对行为序列中的每个 item 进行嵌入,得到稠密向量表示 e(i)。除此之外,其他三组特征:候选item、上下文特征、用户画像特征,同样需要进行嵌入。
Interest Extractor Layer
兴趣提取层,该层使用 GRU来挖掘行为被点击的时序信息,输入为嵌入之后的行为序列 e(i),每时刻都会输出一个隐状态 h(i),表示 i 时刻用户的兴趣表示。使用 GRU 能够挖掘到时序信息,但又丢弃了 DIN 引入的注意力机制,所以 DIEN 又加了第二层 GRU(兴趣变化提取层),并将 Attention 融入其中。
Interest Evolving Layer
Attention
兴趣变化提取层,该层为 GRU + Attention 的组合层,输入来自上层 GRU 输出的隐状态序列,输出只有最后一个 GRU 单元的隐状态 h(T),表示的是从每时刻的用户兴趣中提取的兴趣变化趋势。
Attention 权重的计算公式:
GRU with attentional update gate
将注意力权重 乘到更新门 上,然后再用更新门控制当前信息与历史信息保留的比例。该方式同样需要修改 GRU 单元的计算方式。
目的:给与权重大的隐状态更多的关注。
auxiliary loss
GRU 层存在两个问题,一是在长序列场景中难以充分训练,二是 hidden states 缺少监督,只有最后时刻的隐状态上会产生 loss。
针对这两个问题,文中提出了辅助 loss计算方法,并将其应用在了第一层 GRU 上。如所示, 是在 时刻用户点击的 item, 是 时刻 GRU 输出的隐状态, 是负采样得到的没有被点击的 item。
这样就转换成了判断是否点击的二分类问题,按照下式计算 loss 即可。
优点:
- 引入 GRU 层,挖掘用户兴趣的同时,引入了行为发生的时序信息;
- 引入 GRU 与 Attention 融合层,挖掘用户的兴趣变化趋势。
缺点:
- GRU 层难以训练充分,模型并行性较差,给模型上线带来压力;
- 模型训练复杂度随着行为序列长度的增加而增长。
DSIN
论文链接:DSIN
介绍:
深度会话兴趣网络 DSIN,是将行为序列划分为多个 Session,然后针对每个 Session 去挖掘用户的兴趣以及兴趣变化趋势。在真实场景中,用户短时间内浏览的商品往往比较相似,兴趣比较集中,所以以 Session 为粒度进行兴趣的提取会更加准确。
原理:
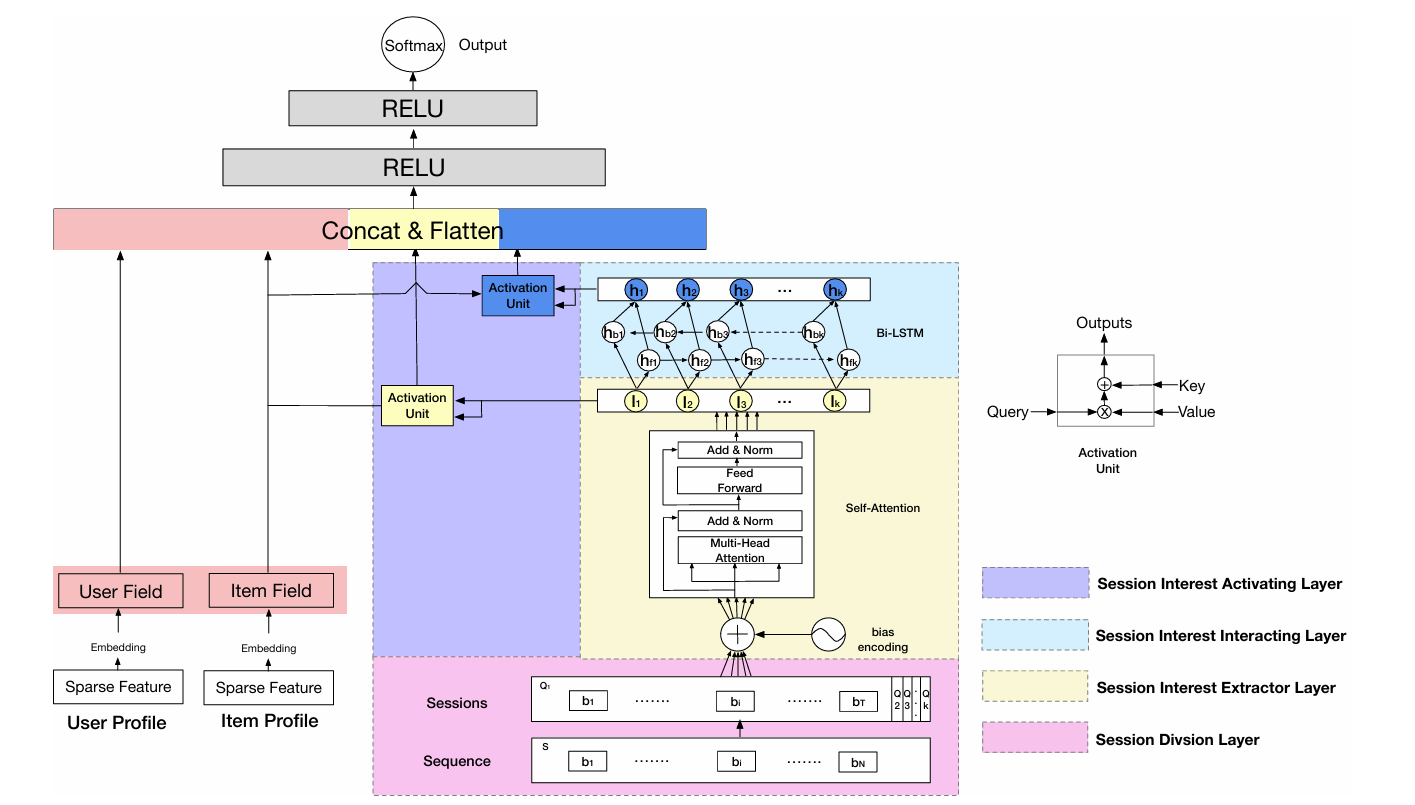
Session Division Layer
该层为会话切分层,用于将行为 Sequence 划分为多个 Session。划分规则是:如果两个行为发生的时间间隔很长或者大于设定的阈值,就可以以此为分割点,这样划分得到的每个 Session 中的行为发生时间比较紧凑,用户的兴趣也会比较集中。
为了保证每个 Session 中行为数量一致,通常会使用截断处理或者 padding。
Session Interest Extractor Layer
该层为会话兴趣提取层,这里使用 Transformer 中的一个 Encoder 单元进行兴趣的提取。因为 Transformer 抛弃了顺序输入的方式,所以模型不会自动考虑输入 Session 的相对位置信息,因此在输入之前需要对 Session 进行位置编码。
Bias Encoding:
跟一般的编码方式不同的是,这里不仅需要对每个 Session 进行位置编码,同时也需要对 Session 中的每个行为进行位置编码,该模块统称为 Bias Encoding。
BE 由三个一维向量累加得到,其中 为 维向量,用于区分 个 Session 的位置差异, 为 T 维向量,用于区分每个 Session 中 T 个行为的位置差异, 为 C 维向量,用于区分每个 C 维行为 embedding 不同维度的位置差异。
向量相加得到形状为 (K,T,C) 的 BE 矩阵,该形状和上层的输出 Q 是一样的,直接相加即可,这样每个会话、会话中的每个行为、行为 embedding 的每个位置都加上了偏置项。
Session Interest Interacting Layer
该层为兴趣交互层,由双层双向LSTM 构成,类似于 DIEN 中的双层 GRU,用于提取用户兴趣的变化趋势。
Session Interest Activating Layer
该层为兴趣激活层,以待推荐的 Item Profile 向量为 Query,分别计算兴趣序列 I 与兴趣变化序列 H 的重要性权重,突出关键兴趣的重要性。权重计算方式采用内积形式,公式如下:
为目标 Item,计算每个兴趣 I 的权重,然后加权累加得到 。
同理,计算每个兴趣变化 H 的权重,然后加权累加得到 。
最后将四部分向量横向拼接,输入全连接做最后的预测即可
优点:
- 以会话粒度进行兴趣的提取,提取结果更精确;
- 利用 Transformer Encoder 挖掘用户兴趣,学习能力更强;
- 引入 双向 LSTM,挖掘用户的兴趣变化趋势;
- 引入 Attention 机制,突出关键行为的重要性。
缺点:
- 引入 Encoder 单元,双层的LSTM,训练复杂度大,给模型上线带来压力。