推荐系统学习（Word2vec）

CBoW & Skip-gram模型架构

2003年，Bengio等人发表了一篇开创性的文章：A neural probabilistic language model[3]。在这篇文章里，他们总结出了一套用神经网络建立统计语言模型的框架（Neural Network Language Model，以下简称NNLM），并首次提出了word embedding的概念，从而奠定了包括word2vec在内后续研究word representation learning的基础。

NNLM模型的基本思想可以概括如下：

  1. 假定词表中的每一个word都对应着一个连续的特征向量；
  2. 假定一个连续平滑的概率模型，输入一段词向量的序列，可以输出这段序列的联合概率；
  3. 同时学习词向量的权重和概率模型里的参数。
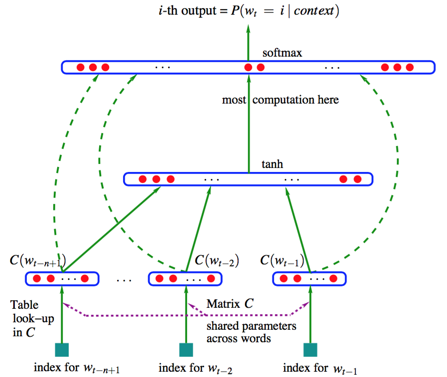
image-20250415000000001

我们可以将整个模型拆分成两部分加以理解：

  1. 首先是一个线性的Embedding层。它将输入的N−1个one-hot词向量，通过一个共享的D×V的矩阵C，映射为N−1个分布式的词向量（distributed vector）。其中，V是词典的大小，D是Embedding向量的维度（一个先验参数）。C矩阵里存储了要学习的word vector。

  2. 其次是一个简单的前向反馈神经网络g。它由一个tanh隐层和一个softmax输出层组成。通过将Embedding层输出的N−1个词向量映射为一个长度为V的概率分布向量，从而对词典中的word在输入context下的条件概率做出预估：

    p(wi∣w1,w2,…,wt−1)≈f(wi,wt−1,…,wt−n+1)=g(wi,C(wt−n+1),…,C(wt−1))p\left(w_{i} \mid w_{1}, w_{2}, \ldots, w_{t-1}\right) \approx f\left(w_{i}, w_{t-1}, \ldots, w_{t-n+1}\right)=g\left(w_{i}, C\left(w_{t-n+1}\right), \ldots, C\left(w_{t-1}\right)\right)

值得注意的一点是，这里的词向量也是要学习的参数。在03年的论文里，Bengio等人采用了一个简单的前向反馈神经网络来拟合一个词序列的条件概率p(wt∣w1,w2,…,wt−1)p\left(w_{t} \mid w_{1}, w_{2}, \ldots, w_{t-1}\right)。但是NNLM存在只能处理定长序列，缺少灵活性的问题，且训练过慢。

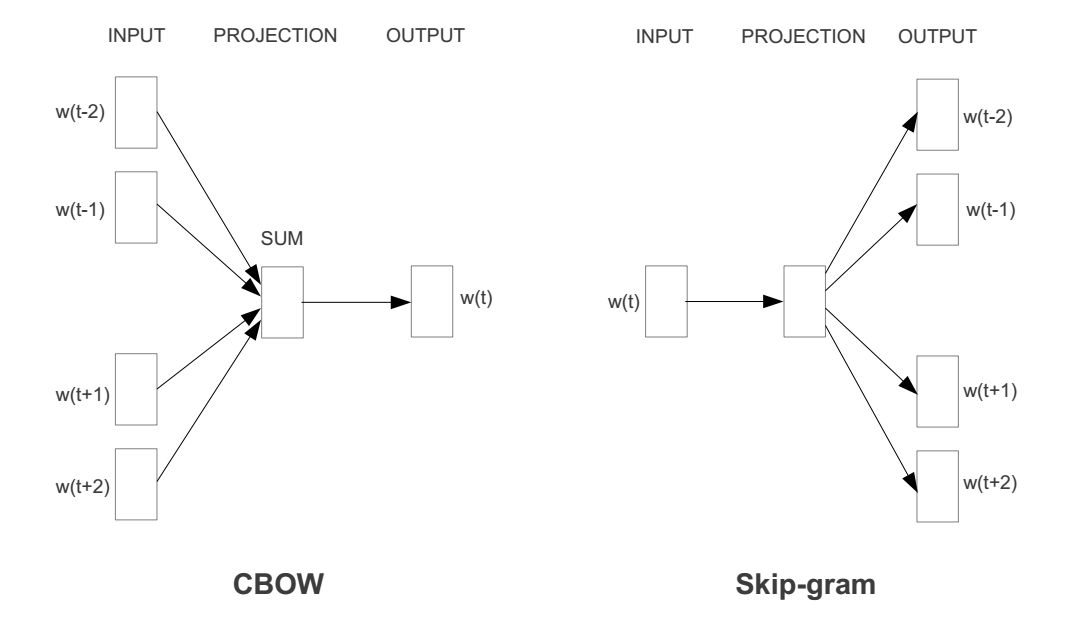
所以Word2vec对原始的NNLM模型做如下改造：

  1. 移除前向反馈神经网络中非线性的hidden layer，直接将中间层的Embedding layer与输出层的softmax layer连接；
  2. 忽略上下文环境的序列信息：输入的所有词向量均汇总到同一个Embedding layer；
  3. 将Future words纳入上下文环境

这样就得到了CBoW模型，将其翻转，也就得到了Skip-gram模型：

image-20250415114926607

损失函数

Skip-gram是通过中心词来推断上下文一定窗口内的单词，中心词center word就是指所给定的词，也就是模型所输入的词；上下文一定窗口内的单词叫做context words，窗口是指window size，也就是指定一个window size的值，所要预测的词语就是和中心词距离在window size内的所有其他词。

在这个模型中，每个词被表示为两个dd维向量，用于计算条件概率。即假设一个词在词典中的索引为ii，当它被当作中心词向量表示为$v_i ∈ R^d ，而为背景词时候向量变送hi为，而为背景词时候向量变送hi为u_i ∈ R^d $ ,设中心词wcw_c在词典中索引为cc，背景词wow_o 在词典中索引为oo，给定中心词生成背景词的条件概率可以通过对向量内积做softmax运算而得到：

P(wo∣wc)=exp⁡(uo⊤vc)∑i∈Vexp⁡(ui⊤vc)P\left(w_{o} \mid w_{c}\right)=\frac{\exp \left(\boldsymbol{u}_{o}^{\top} \boldsymbol{v}_{c}\right)}{\sum_{i \in \mathcal{V}} \exp \left(\boldsymbol{u}_{i}^{\top} \boldsymbol{v}_{c}\right)}

由中心词来推断背景词，注意整个过程的输入是(中心词向量，背景词向量)，根据上面的所提到的背景词之间都是独立的，这种时候，可以把概率写成连乘的形式：

∏t=1T∏−m≤j≤m,j=0P(w(t+j)∣w(t))\prod_{t=1}^{T} \prod_{-m \leq j \leq m, j=0} P\left(w^{(t+j)} \mid w^{(t)}\right)

极大化似然估计的方式，对函数进行变换，从而改变函数的增减性，最终目的是最小化这个函数：

−1T∑t=1T∑−c≤j≤c,j≠0log⁡p(wt+j∣wt)-\frac{1}{T} \sum_{t=1}^{T} \sum_{-c \leq j \leq c, j \neq 0} \log p\left(w_{t+j} \mid w_{t}\right)

当然，也可以展开，改写为：

log⁡P(wo∣wc)=uo⊤vc−log⁡(∑i∈Vexp⁡(ui⊤vc))\log P\left(w_{o} \mid w_{c}\right)=\boldsymbol{u}_{o}^{\top} \boldsymbol{v}_{c}-\log \left(\sum_{i \in \mathcal{V}} \exp \left(\boldsymbol{u}_{i}^{\top} \boldsymbol{v}_{c}\right)\right)

Hierarchical Softmax

使用softmax计算损失，并反向传播更新梯度的过程本质上是一个极大似然估计。在使用softmax计算每个输出的时候，对于每一对样本的时间复杂度为O(V)。在实际情况中，可能遇到的单词单词个数可能非常多，可能高达几十万，所以softmax在计算输出的时候花费的时间复杂度通常是非常高的，为了降低在求取损失函数的的巨大复杂度，Hierarchical Softmax被提出，Hierarchical Softmax可以将时间复杂度降低到O(log(v))。

hierarchical softmax替换的是hidden layer 到 output layer的全连接层部分。

根据词频构建哈夫曼树。如下图所示，假设在这句话中"To become prepared for or as if for选取**“or”**作为输出，选取其他字符作为输入，求解过程如下：

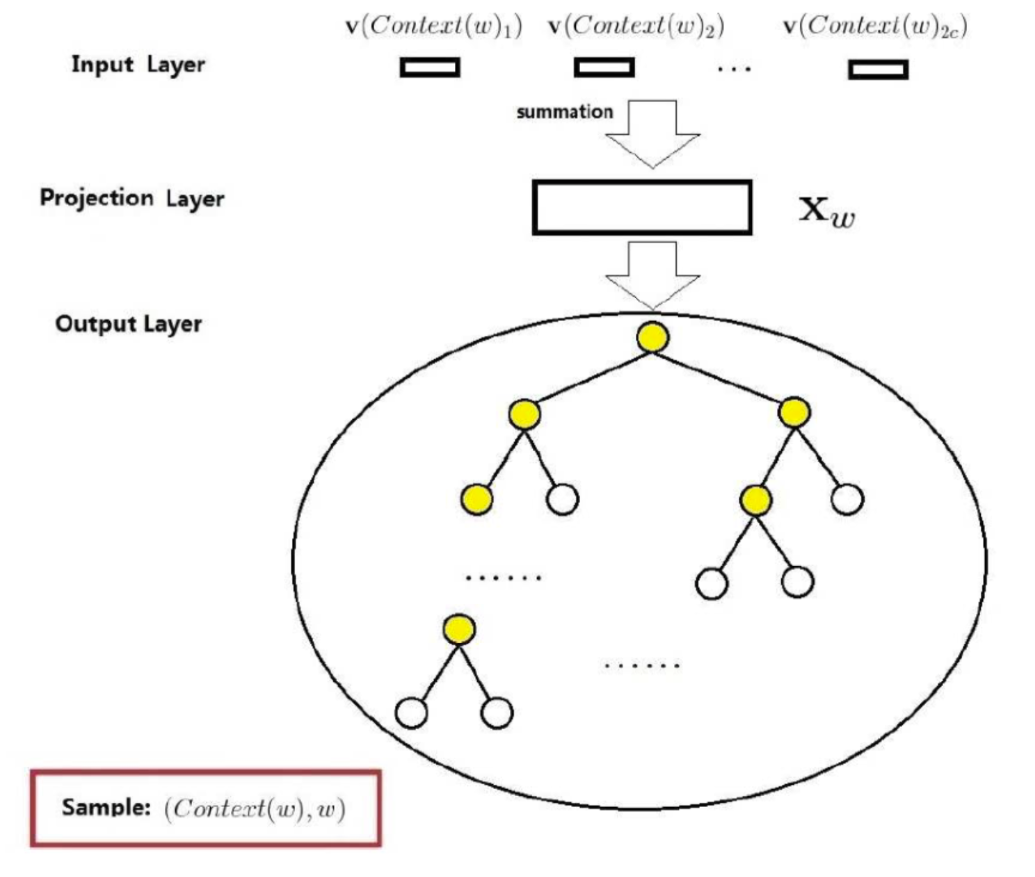
image-20250415161357332
  1. 使用哈夫曼树的贪心策略，在一个自然语言处理数据集中，将每个词的one-hot编码与哈夫曼编码计算出来。
  2. 将{to, become, prepared, for, as ,if, for}的one-hot编码与矩阵 WvnW_{vn} 相乘求平均值,得到 Xw=1CWxn(X1+X2+...Xn)X_w=\frac{1}{C}W_{xn}(X1+X2+...Xn)；
  3. 对于从根节点到目标词汇"or", 有以下路径: p1w,p2w,p3w,p4w,p5wp_1^w,p_2^w,p_3^w,p_4^w,p_5^w······
  4. 路径上的编码有: d2w,d3w,d4w,d5wd_2^w,d_3^w,d_4^w,d_5^w······ ; djwd_j^w 只能取值0或1，路径上的编码连起来也就是每个词汇的哈夫曼编码。
  5. 非叶子节点对应的参数向量： θ1w,θ2w,θ3w,θ4wθ_1^w,θ_2^w,θ_3^w,θ_4^w
  6. lwl^w 代表路径中节点的数量。

对于任意一个节点 θj−1wθ_{j−1}^w 而言，选择左边之路或者右边支路概率为：

p(djw∣Xw,θj−1w)={σ(XTθj−1w),djw=01−σ(XTθj−1w),djw=1p\left(d_{j}^{w} \mid X_{w}, \theta_{j-1}^{w}\right) = \left\{\begin{array}{ll}\sigma\left(X^{T} \theta_{j-1}^{w}\right), & d_{j}^{w} = 0 \\1-\sigma\left(X^{T} \theta_{j-1}^{w}\right), & d_{j}^{w} = 1\end{array}\right.

于是可以给出条件概率：

p(w∣Context⁡(w))=∏j=2lwp(djw∣xw,θj−1w)p(w \mid \operatorname{Context}(w))=\prod_{j=2}^{l^{w}} p\left(d_{j}^{w} \mid \mathbf{x}_{w}, \theta_{j-1}^{w}\right)

同样取对数：

l(w)=∑j=2lw{(1−djw)⋅log⁡[σ(XTθj−1w)]⋅djwlog⁡⋅[1−σ(XTθj−1w)]}l(w)=\sum_{j=2}^{l_{w}}\left\{\left(1-d_{j}^{w}\right) \cdot \log \left[\sigma\left(X^{T} \theta_{j-1}^{w}\right)\right] \cdot d_{j}^{w} \log \cdot\left[1-\sigma\left(X^{T} \theta_{j-1}^{w}\right)\right]\right\}

这个就是Hierarchical Softmax的优化函数，目标是最大化这个函数。

hierarchical softmax设计的初衷是为了用hierarchical的binomial distribution去实现multinomial distribution。这是一种层级实现的softmax，所以叫hierarchical softmax.

负采样

对于机器学习中的分类任务，在训练的时候不但要给正例，还要给负例。对于Hierarchical Softmax，负例是二叉树的其他路径。对于Negative Sampling，负例是随机挑选出来的。利用 (相对简单的) 随机负采样，能大幅度提高性能。用编造的噪声词汇训练的方法被称为Negative Sampling (NEG)。

具体来说，对于每一个输入，除了本身的 label（正样本），同时采样出N个其他 label（负样本），从而我们只需要计算样本在这N+1个 label 上的概率，而不用计算样本在所有 label 上的概率。而在N+1个 label 上计算概率时，不再用 Softmax，而是针对每个 label ，采用逻辑回归的 sigmoid。设计优化目标时，我们希望输出的正样本概率尽可能高，而负样本概率尽可能低。

在 CBOW 中已知词 ww 的上下文 context(w)context(w) ，需要预测 ww ，因此(context(w),w)(context(w),w) 就是一个正样本，context(w)context(w) 和 ww 外的其它词构成负样本。假设已经选取了 mm 个负样本(w,u)(w,u)，其中 u∈NEG(w)=u1,u2,...,umu∈NEG(w)={u_1,u_2,...,u_m}。

  • 对于正样本，CBOW 模型的输出是：pw=σ(xw⊤θw)p^w=σ(x_w^⊤θ^w)

    其中，xw∈RN×1x_w∈R^{N×1} 是 上下文context(w)context(w) 中所有单词的低维词向量的平均值；θw∈RN×1θ_w∈R^{N×1} 是输出层中权重矩阵 W′∈RN×VW^′∈R^{N×V} 中单词 ww 对应的上下文向量。σσ 即 sigmoid 函数。pwp^w 为预测正样本的概率，我们希望 pwp^w 越大越好。

  • 对于负样本，CBOW 模型的输出是：pu=σ(xw⊤θu)p^u=σ(x_w^⊤θ^u)，其中的符号与上面正样本类似。**其意义为负采样修改了原来的⽬标函数。给定中心词的⼀个背景窗口，我们把背景词出现在该背景窗口事件的概率。**我们希望1−pu1-p^u越大越好。

因此，给定一个正样本(context(w),w)(context(w),w) 和它对应的负样本 (context(w),u),u∈NEG(w)(context(w),u),u∈NEG(w) 后，它们的优化目标可设计为：

Lw=pw∏u∈NEG(w)(1−pu)L_w=p^w∏_{u∈NEG(w)}(1−p^u)

同样取对数，设文本序列中时间步 tt 的词 w(t)w(t) 在词典中的索引为 iti_t ，噪声词 wkw_k 在词典中的索引为 hkh_k 。有关以上的对数损失为：

−log⁡P(w(t+j)∣w(t))=−log⁡P(D=1∣w(t),w(t+j))−∑k=1,wk∼P(w)Klog⁡P(D=0∣w(t),wk)=−log⁡σ(uit+j⊤vit)−∑k=1,wk∼P(w)Klog⁡(1−σ(uhk⊤vit))=−log⁡σ(uit+j⊤vit)−∑k=1,wk∼P(w)Klog⁡σ(−uhk⊤vit)\begin{array}{l}-\log P\left(w^{(t+j)} \mid w^{(t)}\right)=-\log P\left(D=1 \mid w^{(t)}, w^{(t+j)}\right)- \\\sum_{k=1, w_{k} \sim P(w)}^{K} \log P\left(D=0 \mid w^{(t)}, w_{k}\right) \\=-\log \sigma\left(u_{i_{t+j}}^{\top} v_{i_{t}}\right)-\sum_{k=1, w_{k} \sim P(w)}^{K} \log \left(1-\sigma\left(u_{h_{k}}^{\top} v_{i_{t}}\right)\right) \\=-\log \sigma\left(u_{i_{t+j}}^{\top} v_{i_{t}}\right)-\sum_{k=1, w_{k} \sim P(w)}^{K} \log \sigma\left(-u_{h_{k}}^{\top} v_{i_{t}}\right)\end{array}

现在，训练中每⼀步的梯度计算开销不再与词典大小相关，而与 采样数K线性相关。当K取较小的常数 时，负采样在每⼀步的梯度计算开销较小。

负采样在标准word2vec的基础上做了两点改进：

  1. 针对softmax运算导致的每次梯度计算开销过⼤，将softmax函数调整为sigmoid函数，当然对应的含义也由给定中心词，每个词作为背景词的概率，变成了给定中心词，每个词出现在背景窗口中的概率

  2. 进行负采样，引入负样本，负采样的名字就是取了第二个改进点。

下采样

除了层次Softmax和负采样的优化算法，Mikolov在13年的论文里还介绍了另一个trick：下采样（subsampling）。其基本思想是在训练时依概率随机丢弃掉那些高频的词：

pdiscard (w)=1−tf(w)p_{\text {discard }}(w)=1-\sqrt{\frac{t}{f(w)}}

其中，tt是一个先验参数，一般取为 1e−51e^{−5}。f(w)f(w)是在语料中出现的频率。

Item2vec的关系

本质上，word2vec模型是在word-context的co-occurrence矩阵基础上建立起来的。因此，任何基于co-occurrence矩阵的算法模型，都可以套用word2vec算法的思路加以改进。

协同过滤算法是建立在一个user-item的co-occurrence矩阵的基础上，通过行向量或列向量的相似性进行推荐。如果我们将同一个user购买的item视为一个context，就可以建立一个item-context的矩阵。进一步的，可以在这个矩阵上借鉴CBoW模型或Skip-gram模型计算出item的向量表达，在更高阶上计算item间的相似度。

参考文献

Word2Vec Tutorial - The Skip-Gram Model · Chris McCormick

Mikolov, Tomas, et al. “Distributed representations of words and phrases and their compositionality.” Advances in neural information processing systems 26 (2013).

Mikolov, Tomas, et al. “Efficient estimation of word representations in vector space.” arXiv preprint arXiv:1301.3781 (2013)