(好久没学习了…)
论文:KuaiFormer: Transformer-Based Retrieval at Kuaishou
这是一篇LLM4Rec的论文,旨在探索大语言模型在推荐系统领域的应用。这篇文章声称从根本上定义检索功能,将传统的得分估计(如CTR预估),转换为Transformer驱动的下一步预测范式,从而实时提取兴趣点,提高检索性能。但也仅仅是使用了LLM的架构,直接以Llama Transformer架构作为Backbone, 并结合快手的业务场景进行训练上的适配和优化。
问题与背景
在短视频推荐系统中,由于短视频内容多样、用户兴趣演变快,传统模型在推荐中存在如下问题:
- 依赖每日更新的模型(PinnerFormer)容易产生“过滤泡沫”效应,使得用户产生审美疲劳。
- 之前已经使用Transformer的架构比如SASRec和Bert4Rec这些将用户行为压缩到单个兴趣向量中,无法准确捕获、反馈全方位用户兴趣。
- 使用胶囊网络等技术的架构虽然从动作序列中提取出多个兴趣向量,但是没有解决长序列带来的性能问题。
同时,在LLM4Rec领域,由于短视频数量较大,也会产生如下几个问题亟待解决:
- 如何训练十亿级别的候选集:LLM的next token是对所有候选词的logits取softmax,但是softmax计算复杂度太高了,肯定不能用。
- 如何让LLM的Transformer捕获多重兴趣:区别于LLM明确的语义方向,用户通常有更多的兴趣点,因此对不同的内容容忍度更高,使得“语义”不同的短视频可能都被视为正方向,对Transformer训练不利。
- 如何更高效地扩展序列长度: Transformer的时间复杂度为O(n2d),与序列长度成平方级关系。在推荐系统中,可以使用更深层次的Hidden layer提高性能,但是请求量远大于LLM,因此需要进行trade-off
为解决在短视频推荐遇到的以上问题,结合快手平台的特点,快手团队提出了KuaiFormer
方法
创新方法概述
- logQ修正的in-batch softmax + 平滑标签:在batch上训练,避免在项目集合上直接训练,然后使用logQ修正采样偏差,最后引入平滑标签
- 引入多个可学习的[CLS] token 提取用户兴趣(利用Bert的思想)
- 自适应序列压缩机制:假设“与最近观看的短视频相比,用户对早期视频的记忆更加模糊”,将较早的项目序列分成几组,将每组压缩为单个表示以减少输入序列长度。然后将这一系列压缩表示与最近的项目。
问题重述
设{(x1,f1),(x2,f2)...,(xn,fn)}为用户的行为序列,其中xi为ID,fi为视频信息(就是特征,包括类似观看时长、互动信息、总时长、标签等)。如果知道用户的xn+1那么目标就可以转化为时序预测问题:
{u1,...,uk}=model({(x1,f1),(x2,f2)...,(xn,fn)})argmaxxn+1∈XP(xn+1∣{u1,...,uk})
模型架构
Embedding 层
Embedding层由两部分组成,第一个是用于处理离散变量(ID这些),第二个是针对连续变量。由于连续变量的先验分布不同,因此设计了分桶策略离散化连续变量(同时保留分布特征)。以短视频时长为例子,就是将大于某个值(此处为300s)之后的均视为一样的特征:
fibucket_dura fidura =int(300min(fidura ,300)∗1000)=LookUp(Fdura ,fibucket_dura )
使用前馈网络作用于离散特征和连续特征的embedding向量,从而生成一个短视频物品的token:
ti=MLP([xi,fi])
最终可以得到序列:{t1,t2,...,tn},然后采用了Llama Transformer架构(RMS范数、multi-head masked self-attention、point-wise 前馈层)
u= Causal_Transformer ({t1,t2,…,tn},L,M)
其中L为transformer参数,M为注意力头的数量。
序列压缩
将序列氛围早中晚三段,早些的项目64个一组,中间的项目16个一组,那么256长度的序列就分成了 2组early序列、5组mid序列、剩下的最近的项目序列:
t1early t2early t1mid t5mid = Mean ( Bi_Transformer ({t1,…,t64},M)= Mean (Bi_Transformer({t65,…,t128},M)= Mean (Bi_Transformer({t129,…,t145},M)…= Mean (Bi_Transformer({t193,…,t208},M)
然后再transformer得到用户兴趣表征,公式中的M表示multi-head的个数:
u= Causal_Transformer (ft1early ,t2early }⊕{t1mid ,…,t5mid }⊕{t209,…,t256},L,M)
多兴趣
借鉴[CLS],用户多兴趣就用 k 个 query进行提取:
{u1,…,uk}= Causal_Transformer (f1early ,t2early }⊕{t1mid ,…,t5mid }⊕{t209,…,t256}⊕{q1,…,qk},L,M)
第n+1个项目 xn+1 的得分取多个兴趣检索的最大值:
P(xn+1∣∣∣∣{u1,…,uk}=∑xX Score x Score xn+1, where Scorexn+1=argmax({xn+1⊤u1,…,xn+1⊤uk})
Softmax加速
借鉴了谷歌RecSys2019的:Sampling-Bias-Corrected Neural Modeling for Large Corpus Item Recommendations
主要思想是,全局softmax计算复杂度太高,那就每次只采样一批,即 in-batch softmax:
L(xn+1)=−log(eScorexn+1+∑xˉn+1BeScorexˉn+1eScorexn+1)
但因为流行度问题,采样又会带来偏差,那就根据采样频率去偏(原文中没有详细说明Q的计算方式,默认是和谷歌一样):
LlogQ=−log(Scorexn+1logQ)=−log(eScorexn+1−log(Qu(xn+1))+∑xˉn+1∈BeScorexˉn+1−log(Qu(xˉn+1))eScorexn+1−log(Qu(xn+1)))
样本的label都是0/1,借鉴When Does Label Smoothing Help,对标签进行平滑:
LlogQsmooth =⎩⎪⎨⎪⎧−(1−α)log( Score xn+1logQ)∑xˉn+1B−∣B∣αlog( Score xˉn+1logQ)
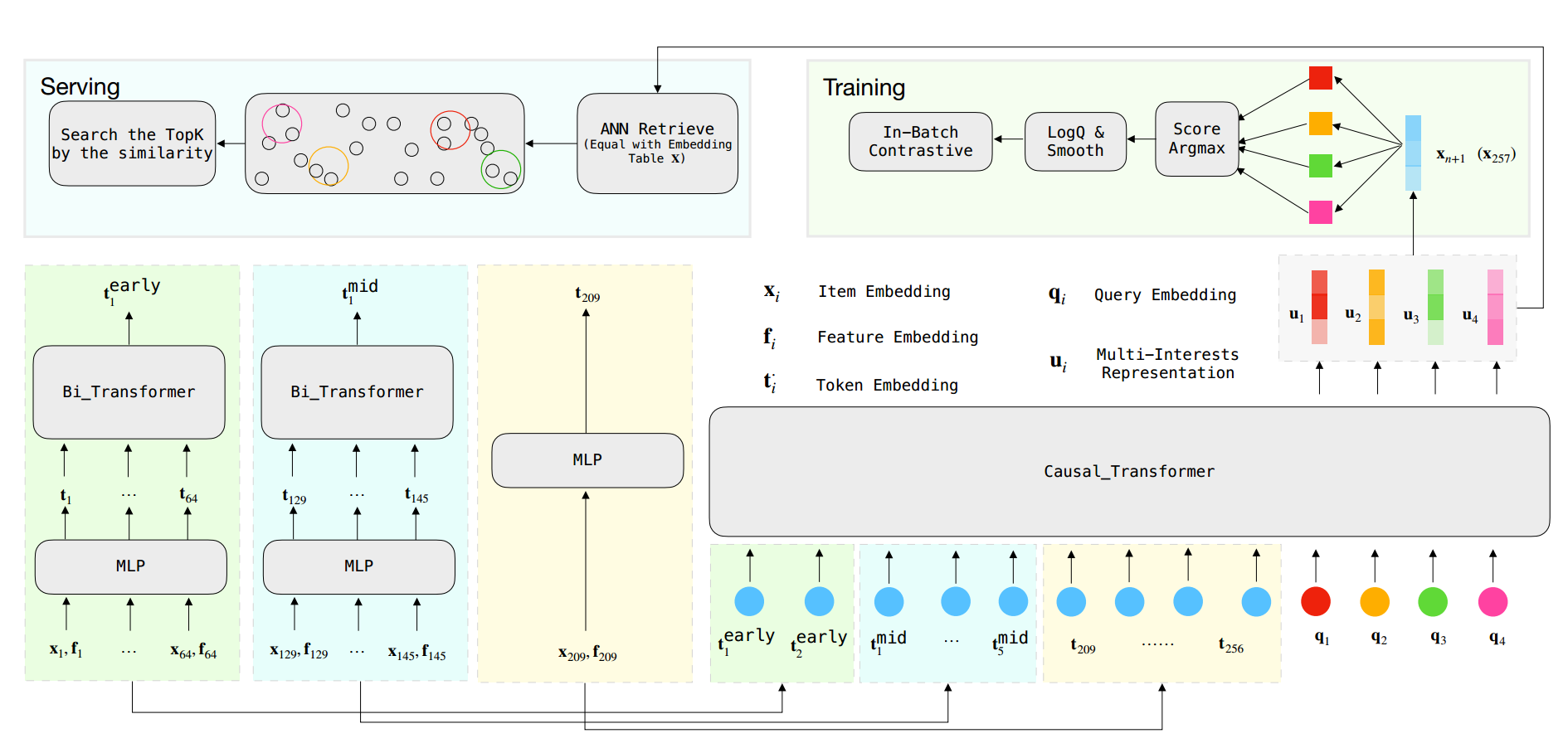
论文总架构如下: